https://github.com/fineman999/algorithm_java/issues/11
Binary Search Tree(BST) · Issue #11 · fineman999/algorithm_java
199. Binary Tree Right Side View 230. Kth Smallest Element in a BST
github.com
https://leetcode.com/problems/binary-tree-right-side-view/
Binary Tree Right Side View - LeetCode
Can you solve this real interview question? Binary Tree Right Side View - Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom. Example 1: [https://asse
leetcode.com
https://leetcode.com/problems/kth-smallest-element-in-a-bst/
Kth Smallest Element in a BST - LeetCode
Can you solve this real interview question? Kth Smallest Element in a BST - Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree. Example 1: [https://assets.leetco
leetcode.com
목차
서론
학부시절에 겉핡기 식으로 배웠던 트리를 이번 기회에 복습하고자 한다.
위의 Leetcode 2문제는 노드 순회를 이용해 문제를 해결한다.
이와 더불어 간단히 BST에 대해 공부하고 BST를 개선한 AVL Tree를 공부하고자 한다.
Binary Search Tree
- 이진 트리(노드의 자식이 최대 두 개인 트리)가 특별한 규칙에 따라 데이터를 저장하는 형태의 자료 구조이다.
- 특별한 규칙으로 다음과 같다.
- 최상위 레벨에 루트 노드가 존재하면서, 각 노드는 최대 2개의 자식 노드를 갖는다.
- 특정 노드를 기준으로 자신의 왼쪽 하위 트리의 모든 노드는 자신보다 작아야 한다.
- 특정 노드를 기준으로 자신의 오른쪽 하위 트리의 모든 노드는 자신보다 크거나 같아야 한다.
이제 구현해 보자.
Node
public class Node<T extends Comparable<T>> implements Comparable<Node<T>>{
public T data;
public Node<T> left;
public Node<T> right;
public Node(T data) {
this.data = data;
this.left = this.right = null;
}
@Override
public int compareTo(Node<T> o) {
return this.data.compareTo(o.data);
}
@Override
public String toString() {
return data.toString();
}
}제네릭을 이용하여 여러 데이터 타입을 사용할 수 있게 하였다.
데이터를 비교하기 위해 Comparable을 implement 받았다.
BinarySearchTree
public class BinarySearchTree<T extends Comparable<T>> {
public Node<T> root;
public BinarySearchTree() {
this.root = null;
}
public void insert(T data) {
root = insert(root, data);
}
public boolean search(T data) {
return search(root, data);
}
public Node<T> delete(T data) {
return delete(root, data);
}
private Node<T> insert(Node<T> node, T data) {
if (Objects.isNull(node)) {
node = new Node<>(data);
return node;
}
if (data.compareTo(node.data) < 0) {
node.left = insert(node.left, data);
} else {
node.right = insert(node.right, data);
}
return node;
}
private boolean search(Node<T> node, T data) {
if (Objects.isNull(node)) return false;
if (data.compareTo(node.data) > 0) return search(node.right, data);
if (data.compareTo(node.data) < 0) return search(node.left, data);
return true;
}
private Node<T> delete(Node<T> node, T data) {
if (Objects.isNull(node)) return null;
if (data.compareTo(node.data) < 0) {
node.left = delete(node.left, data);
} else if (data.compareTo(node.data) > 0) {
node.right = delete(node.right, data);
} else {
if (Objects.isNull(node.left) && Objects.isNull(node.right)) {
node = null;
} else if (Objects.isNull(node.left)) {
node = node.right;
} else if (Objects.isNull(node.right)) {
node = node.left;
} else {
Node<T> temp = findMaxInLeftSubtree(node.left);
node.data = temp.data;
node.left = delete(node.left, temp.data);
}
}
return node;
}
private Node<T> findMaxInLeftSubtree(Node<T> node) {
if (!Objects.isNull(node.right)) {
return findMaxInLeftSubtree(node.right);
}
return node;
}
private void inOrder(Node<T> node, StringJoiner joiner) {
if (node == null) return;
inOrder(node.left, joiner);
joiner.add(node.data.toString());
inOrder(node.right, joiner);
}
/**
* 중위 순회
*/
@Override
public String toString() {
StringJoiner joiner = new StringJoiner(", ", "[", "]");
inOrder(root, joiner);
return joiner.toString();
}
}
삽입
@Test
@DisplayName("insert 테스트")
void insert() {
BinarySearchTree<Integer> bst = new BinarySearchTree<>();
bst.insert(50);
bst.insert(30);
bst.insert(70);
bst.insert(20);
bst.insert(40);
bst.insert(60);
bst.insert(80);
assertThat(bst.toString()).isEqualTo("[20, 30, 40, 50, 60, 70, 80]");
}객체 생성

BinarySearchTree<Integer> bst = new BinarySearchTree<>();에 의해 새로운 객체가 생성된다.
insert(50);

Objects.isNull(node)에 의해 첫 노드가 null를 판별하여 해당 노드에 50을 넣게 된다.
insert(30);
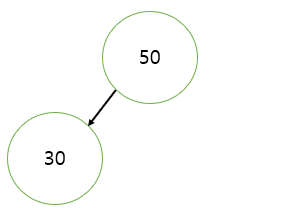
30은 50보다 작기 때문에 data.compare(node.data)<0의 조건에 만족하게 된다.
그렇기 때문에 재귀적으로 현재 노드의 왼쪽으로 값이 이동하게 된다.
왼쪽 노드로 움직이게 된 노드는 현재 null이므로 새로운 객체가 만들어지고 값이 생성한다.
insert(70);

70은 50보다 크기 때문에 오른쪽 노드로 옮겨져서 새로운 노드가 생성된다.
결과

결과로 위와 같이 그래프가 완성되었다.

탐색
@Test
void search() {
BinarySearchTree<Double> bst = new BinarySearchTree<>();
bst.insert(50.1);
bst.insert(30.3);
bst.insert(70.4);
bst.insert(20.5);
bst.insert(40.6);
bst.insert(60.7);
bst.insert(80.8);
assertAll(
() -> assertThat(bst.search(50.1).data).isEqualTo(50.1),
() -> assertThat(bst.search(80.8).data).isEqualTo(80.8)
);
}
이진 탐색 알고리즘을 통해 쉽게 값을 있는지 판별할 수 있다.
- 탐색을 시작할 때는 루트노드부터 시작한다.
- 값을 비교한다.
- 현재 노드가 비어있으면 false을 반환한다.
- 찾는 값이 현재 노드 값보다 크면 오른쪽을 탐색한다.
- 찾는 값이 현재 노드 값보다 작으면 왼쪽을 탐색한다.
- 찾는 값이 현재 노드 값이면 노드를 true를 반환한다.
- 위와 같은 과정을 빈값이나 찾는 값과 현재 노드 값이 일치할 때까지 반복한다.
이러한 특징으로 자식 노드로 내려갈 때마다 검색 공간이 줄어든다.
그래서 평균 탐색 시간 복잡도는 O(logN)이 된다. 하지만 삽입 때 계속해서 왼쪽으로 넣거나 오른쪽으로 넣을 경우 링크드 리스트와 같은 형태를 띠게 된다. 그럴 때는 시간 복잡도가 O(n)이 된다.
삭제
삭제하고 싶은 노드를 탐색하는 과정은 위에서 설명한 것과 같다. 하지만 삭제하고 싶은 노드를 찾았을 때 차이가 있다.
1. 노드가 단말 노드(자식이 없는 노드) 일 경우

현재 노드를 null로 표시하면 된다.
2. 삭제하려는 노드가 자식을 하나만 가지고 있을 경우

이 경우 해당 노드를 삭제하고 자식 노드를 부모 노드의 자식으로 연결한다.
3. 삭제하려는 노드가 자식을 두 개 가지고 있을 경우
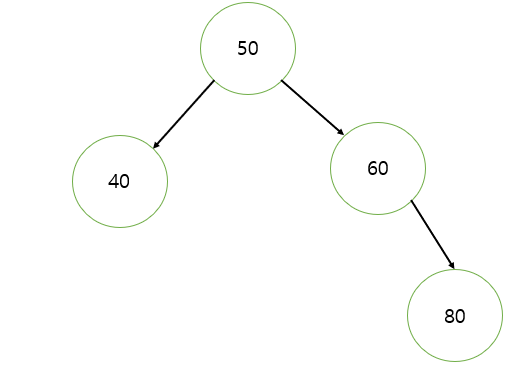
이 경우 왼쪽 서브 트리에서 가장 큰 값을 찾아 해당 노드의 값을 대체(findMaxInLeftSubtree 메서드)하고, 대체한 값을 왼쪽 서브 트리에서 삭제(node.left = delete(node.left, temp.data);)한다.
@Test
void delete() {
BinarySearchTree<Integer> bst = new BinarySearchTree<>();
bst.insert(50);
bst.insert(30);
bst.insert(70);
bst.insert(20);
bst.insert(40);
bst.insert(60);
bst.insert(80);
// 1. 노드가 단말 노드(자식이 없는 노드)일 경우
bst.delete(20);
assertThat(bst.toString()).isEqualTo("[30, 40, 50, 60, 70, 80]");
// 2. 삭제하려는 노드가 자식을 하나만 가지고 있을 경우
bst.delete(30);
assertThat(bst.toString()).isEqualTo("[40, 50, 60, 70, 80]");
// 3. 삭제하려는 노드가 자식을 두개 가지고 있을 경우
bst.delete(50);
assertThat(bst.toString()).isEqualTo("[40, 60, 70, 80]");
}
트리 순회
트리를 순회하는 방법으로 3가지가 있다.
중위 순회

왼쪽 자식 노드 -> 루프 노드 -> 오른쪽 자식 노드 순으로 순회가 이루어진다.
private void inOrder(Node<T> node, StringJoiner joiner) {
if (node == null) return;
inOrder(node.left, joiner);
joiner.add(node.data.toString());
inOrder(node.right, joiner);
}
먼저 왼쪽 서브 트리를 순회하여 작은 값부터 방문한다.
그다음 현재 노드의 데이터를 문자열로 변환하여 StringJoiner에 추가한다. (대부분 출력)
마지막으로 오른쪽 서브 트리를 순회하여 큰 값들을 방문한다.
전위 순회
private void preOrder(Node<T> node, StringJoiner joiner) {
if (node == null) return;
joiner.add(node.data.toString());
preOrder(node.left, joiner);
preOrder(node.right, joiner);
}루프 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드 순으로 순회가 이루어진다.
후위 순회
private void postOrder(Node<T> node, StringJoiner joiner) {
if (node == null) return;
postOrder(node.left, joiner);
postOrder(node.right, joiner);
joiner.add(node.data.toString());
}오른쪽 자식 노드 -> 왼쪽 자식 노드 -> 루프 노드 순으로 순회가 이루어진다.
230. Kth Smallest Element in a BST
알고리즘 설명
k번째로 작은 값을 찾는 문제이다.
알고리즘 풀이
class Solution {
int count = 0;
int k = 0;
int result = Integer.MAX_VALUE;
public int kthSmallest(TreeNode root, int k) {
count = 0;
this.k = k;
inorder(root);
return result;
}
private void inorder(TreeNode root) {
if (root == null) return;
inorder(root.left);
count++;
if (count == k)
result = root.val;
inorder(root.right);
}
}위에서 구현한 inOrder를 이용하면 된다.
BST를 중위 순회하면 노드들이 오름차순으로 정렬되어 나오므로 중위 순회를 통해 문제를 해결할 수 있다.

199. Binary Tree Right Side View
알고리즘 설명
이진트리의 오른쪽에서 볼 수 있는 노드들을 찾는 문제이다.
즉, 각 레벨에서 가장 오른쪽에 있는 노드들을 찾아서 리스트로 반환하는 것이 목표이다.
class Solution {
private List<Integer> result = new ArrayList<>();
public List<Integer> rightSideView(TreeNode root) {
preorder(root, 0);
return result;
}
private void preorder(TreeNode root, int depth) {
if (root == null) return;
if (result.size() <= depth)
result.add(root.val);
else {
result.remove(depth);
result.add(depth, root.val);
}
preorder(root.left, depth + 1);
preorder(root.right, depth + 1);
}
}위에서 구현한 preOrder를 이용할 수 있다.
전위 순회를 수행하면서 각 레벨에서 처음 방문하는 노드를 결과 리스트에 추가하고, 같은 레벨의 다른 노드들은 결과 리스트에서 덮어씌우는 방식으로 구현하였다.

결론
이번 기회에 BST를 정리하면서 회고하는 시간을 가졌다. 이진 탐색 트리는 탐색에서 링크드 리스트보다 빠른 속도를 가지고 있다. 하지만 자칫하면 링크드 리스트와 같이 단방향으로 트리가 생성될 수 있다는 단점이 있다. 그래서 BST를 개선한 AVL Tree, B+tree 등이 있다.
'자료구조' 카테고리의 다른 글
| Hash Collision & Open Addressing - Linear Probing Hash Table (5) | 2023.09.03 |
|---|
