Hash Collision & Open Addressing - Linear Probing Hash Table
https://github.com/fineman999/algorithm_java/issues/10
HashMap & Hash collision · Issue #10 · fineman999/algorithm_java
github.com
1. 서론
원티드 프리온보딩 2주 차 2번째 과제로 Linear Probing 방식의 Hash Table를 구현하는 과제가 주어졌다.
해시 테이블에서는 충돌이 발생할 수 있는 데 해결 방법으로 두 가지를 나눌 수 있다.
첫 번째로 Seperate Chaing이 있다. Sepearte Chaing은 충돌이 일어나는 bucket에서 새로운 공간(overflow enties)을 연결해서 저장하는 방식으로 해시 충돌을 방지할 수 있다.
두 번째로 Open Addressing이 있다.
Seperate Chaing 방식과 달리 추가 공간을 사용하지 않고 충돌을 해결하는 방법이다.
Open Addressing을 하는 방법으로 Linear Probing(선형 탐색), 이차원 탐색(Quadratic Probling), 더블 해싱(Double Hashing)이 있다.
여기서 중점적으로 다룰 것은 Linear Probing 방식의 Hash Table이다.
2. Linear Probing 방식의 Hash Table

Linear Probling은 해시 테이블의 충돌을 해결하기 위한 컴퓨터 프로그래밍 방식, 키-값 쌍의 컬렉션을 유지 관리하고 주어진 키와 관련된 값을 찾기 위한 데이터 구조이다.
해시 테이블에 충돌이 발생하면 그다음 메모리 주소 다음 위치의 Bucket(Key-value pairs)을 저장/검색할 수 있다.
이러한 특징 때문에 데이터가 Key의 해시 결과 반환되는 Bucket의 인덱스와 일치하는 주소에 저장된다는 보장은 없다. 그러므로 구현할 때 주의해서 작성해야한다.
이제 코드를 작성해보자.
2.1 Entry Class
public class Entry<K, V> {
K key;
V value;
Entry(K key, V value) {
this.key = key;
this.value = value;
}
}제네릭을 이용하여 해당 값을 찾을 Key와 Key를 통해 값을 찾을 value를 정의하였다.
2.2 LinearProbingHashTable Class
public class LinearProbingHashTable<K, V> {
private final Entry<K, V>[] table;
private int numberOfItems;
public LinearProbingHashTable(int capacity) {
table = new Entry[capacity];
numberOfItems = 0;
}
private int hash(Object key) {
return key.hashCode() % table.length;
}
public void put(K key, V value) {
int indexOfBucket = this.hash(key);
while (table[indexOfBucket] != null) {
if (table[indexOfBucket].key.equals(key)) {
table[indexOfBucket].value = value;
return;
}
indexOfBucket = (indexOfBucket + 1) % table.length;
}
table[indexOfBucket] = new Entry<>(key, value);
numberOfItems++;
}
public V get(K key) {
int indexOfBucket = this.hash(key);
while (table[indexOfBucket] != null) {
if (table[indexOfBucket].key.equals(key)) {
return table[indexOfBucket].value;
}
indexOfBucket = (indexOfBucket + 1) % table.length;
}
return null;
}
public Entry<K, V> remove(K key) {
if (isEmpty()) {
throw new RuntimeException("Table is empty");
}
int indexOfBucket = this.hash(key);
while (table[indexOfBucket] != null) {
if (table[indexOfBucket].key.equals(key)) {
Entry<K, V> retunEntry = table[indexOfBucket];
table[indexOfBucket] = null;
numberOfItems--;
return retunEntry;
}
indexOfBucket = (indexOfBucket + 1) % table.length;
}
return null;
}
public boolean isEmpty() {
return numberOfItems == 0;
}
}LinearProbling을 이용하여 Hash Table를 구현하였다.
주요 구성 요소와 메서드의 설명은 다음과 같다.
1. LinearProbingHashTable<K, V> 클래스
- 제네릭(Generic)으로 작성되어, 다양한 키와 값 유형을 처리할 수 있다.
- 해시 테이블은 Entry<K, V> 배열로 구현되며, 이 배열의 크기는 초기 생성자에서 지정된다.
2. hash(Object key) 메서드
- 이 메서드는 주어진 키의 해시 코드를 계산하여 배열 인덱스로 변환한다. 해시 함수로 키의 해시 코드를 사용하여 버킷을 결정한다.
3. put(K key, V value) 메서드
- 주어진 키와 값을 해시 테이블에 추가한다.
- 충돌이 발생하면 LinearProbing을 사용하여 다음 빈 버킷을 찾는다.
- 만약 이미 같은 키가 존재한다면 해당 키의 값(value)을 업데이트한다.
4. get(K key) 메서드
- 주어진 키에 해당하는 값을 검색한다.
- LinearProbing를 사용하여 해당 키를 가진 버킷을 찾는다.
5. remove(K key) 메서드
- 주어진 키에 해당하는 항목을 해시 테이블에서 제거하고 반환한다.
- LinearProbing를 사용하여 해당 키를 가진 버킷을 찾아 제거한다.
6. isEmpty() 메서드
- 해시 테이블이 비어있는지 여부 확인
2.3 테스트
이제 정상적으로 작동하는지 테스트를 해보자
class LinearProbingHashTableTest {
@Test
@DisplayName("충돌이 발생할 경우 다음 버킷에 저장")
void test() {
LinearProbingHashTable<Object, Object> hashTable = new LinearProbingHashTable<>(10);
hashTable.put("강호동", "010-1111-1111");
hashTable.put("유재석", "010-2222-2222");
hashTable.put("신동엽", "010-3333-3333");
assertAll(
() -> assertThat(hashTable.get("강호동")).isEqualTo("010-1111-1111"),
() -> assertThat(hashTable.get("유재석")).isEqualTo("010-2222-2222"),
() -> assertThat(hashTable.get("신동엽")).isEqualTo("010-3333-3333")
);
}
}
LinearProblingHashTable의 용량을 10으로 설정하고 값을 넣었다.
이제 Debug를 통해 충돌이 발생했을 경우 다음 버킷에 저장되는지 확인해 보자.
1. hashTable.put("강호동", "010-1111-1111")

현재 강호동의 hashCode는 4로 되어있다. 현재는 아무런 값이 저장되어 있지 않으므로 while문 내부를 접근하지 않고 새로운 객체를 생성하게 된다.
2. hashTable.put("유재석", "010-2222-2222");

유재석의 hashcode는 9이므로 정상적으로 값이 넣어졌다.
3. hashTable.put("신동엽", "010-3333-3333");
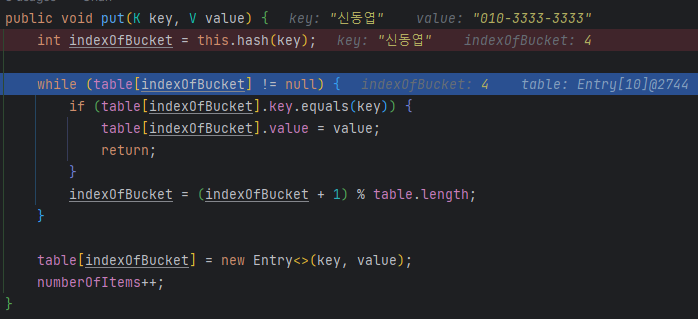
신동엽의 hashcode는 4이므로 이전의 강호동의 hashcode와 일치한다.
그럼 while문 내부를 접근하게 된다.

이전에 저장된 강호동의 값과 일치하지 않으므로 indexOfBucket의 값은 +1 된다.

iwhile 문을 빠져나오고 새로운 객체가 테이블에 생성되었고 numberOfItems가 3이 되었다.
4. 테스트 결과

2.4 문제점
1. remove
@Test
@DisplayName("키값을 제거한 다음 Linear Probing에 의해 생성된 키 값을 가져올 경우")
void remove() {
LinearProbingHashTable<Object, Object> hashTable = new LinearProbingHashTable<>(10);
hashTable.put("강호동", "010-1111-1111");
hashTable.put("유재석", "010-2222-2222");
hashTable.put("신동엽", "010-3333-3333");
hashTable.remove("강호동");
assertAll(
() -> assertThat(hashTable.get("유재석")).isEqualTo("010-2222-2222"),
() -> assertThat(hashTable.get("신동엽")).isEqualTo("010-3333-3333")
);
}
키값을 제거한 다음 경우 Linear Probing에 의해 생성된 키 값을 가져올 경우에 에러가 발생하고 있다.
기존에 저장된 키를 제거하면 그 해당되는 bucket은 null 된다.
그리고 같은 hashcode를 가진 값을 조회하면 remove 한 다음 bucket에 저장되어 있기 때문에 값을 불러오지 못하고 null을 반환하게 된다.
2. 용량 초과
@Test
@DisplayName("용량을 초과할 경우")
void test2() {
LinearProbingHashTable<Object, Object> hashTable = new LinearProbingHashTable<>(5);
hashTable.put("강호동", "010-1111-1111");
hashTable.put("유재석", "010-2222-2222");
hashTable.put("신동엽", "010-3333-3333");
hashTable.put("이수근", "010-4444-4444");
hashTable.put("이광수", "010-5555-5555");
hashTable.put("송지효", "010-6666-6666");
assertAll(
() -> assertThat(hashTable.size()).isEqualTo(6),
() -> assertThat(hashTable.getCapacity()).isEqualTo(10),
() -> assertThat(hashTable.get("이수근")).isEqualTo("010-4444-4444"),
() -> assertThat(hashTable.get("강호동")).isEqualTo("010-1111-1111"),
() -> assertThat(hashTable.get("유재석")).isEqualTo("010-2222-2222"),
() -> assertThat(hashTable.get("신동엽")).isEqualTo("010-3333-3333")
);
}
현재 프로덕션 코드에서 put 메서드는 null 값을 찾아서 객체를 생성하는 로직이다. 그런데 null 인 값이 없으므로 무한 루프에 빠지게 되었다.
위와 같은 문제를 해결하기 위해 Load Factor와 동적 리사이징을 사용하는게 좋다.
Load Factor는 해시 테이블에 저장된 항목의 수를 해시 테이블의 전체 크기로 나눈 값으로, 해시 테이블의 "가득 찬 정도"를 나타낸다. 즉 Load Factor가 0.5이면 해시 테이블의 절반만 항목으로 채워져 있다는 것을 의미한다. Open Addressing 방법에서는 Load Factor가 증가하면 해시 테이블 내의 사용 가능한 빈 슬롯이 줄어들게 된다. 이로 인해 충돌의 수가 증가하여 성능 저하를 일으킬 수 있다.
Open Addressing에서는 Load Factor가 너무 높아지면 성능이 크게 저하될 수 있으므로 일반적으로 임계값을 0.5 또는 0.6으로 한다.
동적 리사이징은 해시 테이블의 크기를 동적으로 조정하는 과정이다. 특정 임계값을 초과할 가능성이 있을 경우 테이블의 크기를 증가시켜(보통 2배로) 새로운, 더 큰 배열에 기존의 데이터를 재해시하여 저장하게 된다.
3. 리팩토링
public class LinearProbingHashTable<K, V> {
private static final float LOAD_FACTOR = 0.6f;
private Entry<K, V>[] table;
private int numberOfItems;
private static final Object REMOVED = new Object();
@SuppressWarnings("unchecked")
public LinearProbingHashTable(int capacity) {
table = new Entry[capacity];
for (int i = 0; i < capacity; i++) {
table[i] = new Entry<>(null, null);
}
numberOfItems = 0;
}
private int hash(K key) {
return key.hashCode() % table.length;
}
public void put(K key, V value) {
int indexOfBucket = this.hash(key);
while (table[indexOfBucket].key != null) {
if (table[indexOfBucket].key.equals(key)) {
table[indexOfBucket].value = value;
return;
}
indexOfBucket = (indexOfBucket + 1) % table.length;
}
table[indexOfBucket] = new Entry<>(key, value);
numberOfItems++;
if (isResizingRequired()) resize();
}
public V get(K key) {
int indexOfBucket = this.hash(key);
while (table[indexOfBucket].key != null || table[indexOfBucket].key == REMOVED) {
if (table[indexOfBucket].key.equals(key)) {
return table[indexOfBucket].value;
}
indexOfBucket = (indexOfBucket + 1) % table.length;
}
return null;
}
@SuppressWarnings("unchecked")
public void remove(K key) {
if (isEmpty()) {
throw new RuntimeException("Table is empty");
}
int indexOfBucket = this.hash(key);
while (table[indexOfBucket] != null) {
if (table[indexOfBucket].key.equals(key)) {
table[indexOfBucket].key = (K) REMOVED;
table[indexOfBucket].value = null;
numberOfItems--;
return;
}
indexOfBucket = (indexOfBucket + 1) % table.length;
}
}
public boolean isEmpty() {
return numberOfItems == 0;
}
private boolean isResizingRequired() {
return (float) numberOfItems / table.length > LOAD_FACTOR;
}
@SuppressWarnings("unchecked")
private void resize() {
Entry<K, V>[] oldTable = table;
int resizeLength = table.length * 2;
table = new Entry[resizeLength];
numberOfItems = 0;
for (int i = 0; i < resizeLength; i++) {
table[i] = new Entry<>(null, null);
}
for (Entry<K, V> entry : oldTable) {
if (entry.key != null && entry.key != REMOVED) {
put(entry.key, entry.value);
}
}
}
public int size() {
return numberOfItems;
}
public int getCapacity() {
return table.length;
}
}@SuppressWarnings("unchecked")
참고로 @SuppressWarnings("unchecked")은 없으면 Entry<K,V>인 제네릭을 배열로 선언했기 때문에 힙 오염이 발생할 수 있는 것을 비검사 경고라고 알려준다.
하지만 Entry<K,V>을 직접적으로 다루지 않고 LinearProbingHashTable로 간접적으로 다루기 때문에 힙 오염이 발생하지 않으므로 @SuppressWarnings("unchecked") 통해 비검사 경고를 제거할 수 있다.
이제 변경된 주요 메서드와 생성자를 알아보자.
1. LinearProbingHashTable(int capacity)
- for문이 추가되었다. 이전에는 정확하게 capacity를 체크하지 않고 null이 아닌 현재 entry가 존재하는 것만 합쳐서 길이를 측정하였다. 그래서 null도 포함시키기 위해 for문을 추가하였다.
2. 추가된 필드 값
- LOAD_FACTOR: 해시 테이블 크기를 조절하기 위한 임계값으로, 0.6으로 정의하였다.
- REMOVED: 삭제된 항목을 나타내는 객체이다.
3. put(K key, V value) 메서드
- 필요한 경우 해시 테이블의 크기를 늘릴 수 있도록 resize() 메서드를 정의하였다.
4. isResizingRequired() 메서드
- 해시 테이블의 크기를 조정한다.
5. resize() 메서드
- 해시 테이블을 크기를 두 배로 늘린다.
- key값이 null이거나 REMOVED가 아닐 경우에만 키와 함께 값을 넣는다.
- 이때 모든 기존 항목을 새로운 크기에 맞게 다시 해싱한다.
6. remove(K key)
- 삭제된 항목의 Key에 (K) REMOVED를 추가하여 null이 들어가지 못하게 만든다.
4. 결론

Linear Probing 방식을 사용하여 충돌을 처리하고, 필요한 경우 해시 테이블의 크기를 동적으로 조절할 수 있게 구현했다. 또한 제네릭으로 작성되어 다양한 데이터 유형을 다룰 수 있으며, 삭제된 항목을 특별한 객체로 표시하여 get 메서드에서의 예외 상황을 방지하게 구현하였다.